[Tensorflow] Simple Linear Regression(단순 선형 회귀) 개념과 구현

Simple Linear Regression (단순 선형 회귀)

머신러닝 공부를 위해 주피터 개발환경을 모두 세팅하고 처음 배우는 것은 선형 회귀. 간단한 선형 회귀를 구현해보자.

'선형 회귀' 말만 들으면 정말 어렵다. 수학적으로 이해하자면 어떤 변수의 값에 따라서 특정 변수의 값이 영향을 받는 것이다. 단순 선형 회귀 분석(Simple Linear Regression Analysis)이란 변수 x(독립변수), 변수 x에 의해 값이 종속적인 변수 y를 놓고 이 둘의 선형 관계를 모델링하는 것이다. 이때 x의 개수가 1개면 그것이 단순 선형 회귀이다.

y = Wx + b

위 수식은 단순 선형 회귀의 수식이다. x는 독립변수, W는 곱해지는 값(머신러닝에서는 가중치; weight), 별도로 더하는 값 b는 편향(bias)이다. 결국 w, x, b로 직선의 방정식을 표현한 것이고, W가 직선의 기울기, b가 절편이다.

결국 W와 b의 값을 적절히 찾아내는 것이 x와 y의 관계를 적절히 모델링한 것이 된다.

적절한 W와 b를 찾기 위해 cost(비용)라는 개념이 등장한다. 이는 간단하게 점과 선의 차이이다. 우리가 기대하는 선과 데이터 점의 차이값, 즉 cost를 최소화하는 것이 궁극적인 목표이다. 이것을 minimize cost라고 한다. cost의 식은 다음과 같다.

H(x)와 y의 값의 차이가 점과 선의 차이 cost이다. 시그마(합) 안에 제곱이 있는 이유는 점이 선 밑에 있으면 음수이기 때문에 모두 양수로 취급해서 cost를 계산한다.

이제 텐서플로에서 선형 회귀를 구현할 것인데 cost의 개념이 잡히지 않으면 이해가 어려울 수 있다. (필자가 그랬다) 정말 쉽게 말하자면 우리는 y=x, 즉 W가 1이고 b가 0인 선을 기대하고 x에 1, 2, 3을 주고 y에 1, 2, 3을 준다. 그리고 W와 b의 값을 처음에 랜덤하게 주면 아무 선이 그이고, 이 선을 기준으로 점과의 cost를 줄이는 것을 머신러닝을 통해 구현하는 것이다.

---

텐서플로에서 구현하기

주피터 노트북을 열고 새 파이썬 파일을 작성한다.

import tensorflow as tf import numpy as np x_train = [1,2,3] y_train = [1,2,3] W = tf.Variable(tf.random.normal((1,))) b = tf.Variable(tf.random.normal((1,))) hypothesis = x_train * W + b cost = tf.reduce_mean(tf.square(hypothesis - y_train)) optimizer = tf.train.GradientDescentOptimizer(learning_rate = 0.01) train = optimizer.minimize(cost) sess = tf.Session() sess.run(tf.global_variables_initializer()) for step in range(2001):     sess.run(train)     if step % 200 == 0:         print(step, sess.run(cost), sess.run(W), sess.run(b))

cs

코드를 하나씩 살펴보자.

import tensorflow as tf import numpy as np

cs

텐서플로를 사용할 것이기에 당연히 import해주고 numpy도 import한다. numpy(넘파이)는 파이썬을 통한 데이터 분석을 할 때 기초 라이브러리로 사용된다. array 단위(행렬 단위)로 데이터에 대한 연산을 수행한다. W, b의 값을 랜덤하게 주기 위해서 사용하는 random.normal도 numpy에 포함되어 있다.

x_train = [1,2,3] y_train = [1,2,3]

cs

x와 y의 값을 선언한다. 결국 점들을 연결하면 y=x의 그래프가 만들어질 것이다.

W = tf.Variable(tf.random.normal((1,))) b = tf.Variable(tf.random.normal((1,)))

cs

weight(기울기), bias(절편)을 numpy를 이용해 랜덤 하나씩 선언한다. Variable은 텐서플로에서 사용하는 변수를 선언할 때 사용한다.

hypothesis = x_train * W + b

cs

hypothesis(가설)를 선언한다. 이것이 우리가 긋는 선이다. 당연히 W, b를 랜덤하게 선언했기 때문에 기대하는 값과는 맞지 않을 것.

cost = tf.reduce_mean(tf.square(hypothesis - y_train))

cs

위에서 본 cost 수식을 텐서플로 함수를 통해 선언한다. 선(h(x))과 점(y)의 차이를 square(제곱)해서 reduce_mean(갯수로 나눠서 평균 도출)한다.

optimizer = tf.train.GradientDescentOptimizer(learning_rate = 0.01) train = optimizer.minimize(cost) sess = tf.Session() sess.run(tf.global_variables_initializer())

cs

cost를 최소화하기 위해 W, b를 찾는 알고리즘 중 Gradient Descent (경사 하강) 알고리즘을 사용할 것이다. 이를 이해하기 위해서 그래프를 보자.

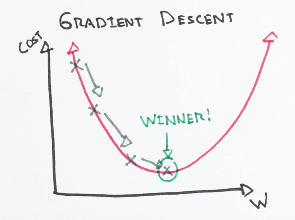
x축이 w, y축이 cost이다. 결국 극소점이 궁극적인 목표 minimize cost인 상태이다. 처음 랜덤하게 W, b를 선언하고 그 지점에서의 gradient(기울기)를 통해 cost가 작아지는 지점(기울기가 0이 될 수 있게)으로 값의 변화를 차차 준다. learning_rate 변수로 계산된 gradient 값을 얼마만큼 반영할 지 정한다. learning_rate가 클 수록 한번의 변화가 커지는 것인데 이게 너무 크면 값이 튄다. (Overfitting Issue) learning_rate는 0.01~0.1정도로 놓는 것이 일반적이다.

optimizer를 선언하고 cost를 minimize하기 위한 함수 minimize를 사용해서 train을 선언한다. 세션에서 그래프를 시작하기 위해 tf 내 Session 함수로 sess를 초기화한다. 그리고 전역 변수를 초기화한다.

for step in range(2001):     sess.run(train)     if step % 200 == 0:         print(step, sess.run(cost), sess.run(W), sess.run(b))

cs

for문을 선언해서 2000번 머신러닝을 시작한다. 포문이 돌 때마다 sess.run(train)을 통해 경사하강법을 토대로 cost를 minimize한다. 그리고 그 결과를 출력하는데, 2000줄은 너무 많으니 0부터 200의 배수 단위로 10줄 출력한다.

2000번의 러닝 끝에 W와 b가 각각 1과 0에 거의 도달했음을 알 수 있다.

텐서플로 머신러닝 공부 중 가장 기본적인 단순 선형 회귀를 구현해보았다.

---

tip...

주피터에서 한번 run하면 학습한 결과가 저장되기 때문에 코드의 변경 후 학습을 다시 시작하고 싶다면 저장 후 해당 파이썬 파일을 shutdown하고 다시 들어가서 실행하자.